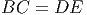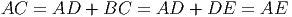Выходной тест 10 класса. Вариант 1.

Вариант 1.

 

  • Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй автомобиль проехал первую половину пути со скоростью, меньшей скорости первого на 15 км/ч, а вторую половину пути со скоростью 90 км/ч, в результате чего прибыл в в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 54 км/ч. Ответ дайте в км/ч.
  • Сократите дробь
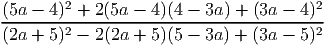
    2 2 (5a---4)-+-2-(5a----4)(4---3a-) +-(3a---4)- (2a + 5)2 - 2(2a + 5)(5 - 3a ) + (3a - 5)2
  • Решите уравнение
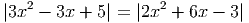
    |3x2 - 3x + 5| = |2x2 + 6x - 3|
  • Найдите cos α, если cos(60∘ + α) = -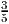3 5, 120∘ < α < 210∘
  • Найдите площадь треугольника, ограниченного линиями y = x - 2,y = -x - 2,y = 0.
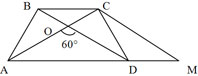
  • В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60∘. Докажите, что трапеция - равнобедренная.
  • Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй автомобиль проехал первую половину пути со скоростью, меньшей скорости первого на 15 км/ч, а вторую половину пути со скоростью 90 км/ч, в результате чего прибыл в в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 54 км/ч. Ответ дайте в км/ч.
    Решение: Обозначим за x скорость первого автомобиля. Тогда весь путь он прошел за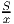 S- x часов. Путь второго автомобиля состоит из двух половин, первую он ехал со скоростью, меньшей скорости первого на 15 км/ч, значит она потратил 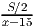xS-∕125 часов, аналогично на вторую половину пути он потратил 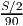S9∕02 часов. Так как автомобили в пункт B прибыли одновременно, то их время в пути совпадает. 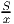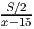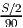S- x = S∕2- x- 15 + S∕2 90. Домножим обе части равенства на 2 и сократим S. Получим уравнение
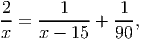
    -2 = ---1---+ 1-, x x - 15 90
    решить которое не составляет труда.
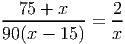
    75 + x 2 ----------- = -- 90 (x - 15) x
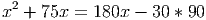
    x2 + 75x = 180x - 30 * 90
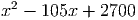
    2 x - 105x + 2700
    Решая квадратное уравнение, получаем два корня
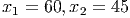
    x = 60,x = 45 1 2
    По условию, скорость больше 54 км/ч.
    Ответ: Скорость первого автомобиля 60 км/ч.
  • Сократите дробь
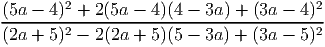
    2 2 (5a---4)-+-2-(5a----4)(4---3a-) +-(3a---4)- (2a + 5)2 - 2(2a + 5)(5 - 3a ) + (3a - 5)2
    Решение: Заметим, что в числителе и знаменателе стоит квадрат суммы/разности.
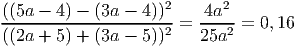
    ((5a - 4) - (3a - 4))2 4a2 ((2a +-5) +-(3a---5))2-= 25a2-= 0,16
    Легко убедиться, что если в числителе квадрат разности заменить на квадрат суммы, то ответ не изменится. Аналогично в знаменателе.
    Ответ: 0,16
  • Решите уравнение
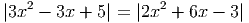
    |3x2 - 3x + 5| = |2x2 + 6x - 3|
    Решение: Вспомним, что если |f(x)| = |g(x)|, то модули раскрываются всего двумя способами f(x) = g(x) и f(x) = -g(x). В первом случае получаем
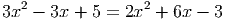
    3x2 - 3x + 5 = 2x2 + 6x - 3
    2 x - 9x + 8 = 0
    x = 1,x = 8. 1 2
    Во втором случае
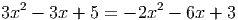
    3x2 - 3x + 5 = - 2x2 - 6x + 3
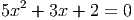
    2 5x + 3x + 2 = 0
    D < 0,
    решений нет.
    Ответ: 1; 8
  • Найдите cos α, если cos(60∘ + α) = -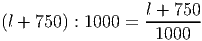3 5, 120∘ < α < 210∘
    Решение: Обозначим угол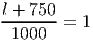
    60 + α = ϕ,
    тогда
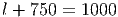
    120 + 60 < ϕ < 210 + 60
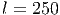
    180 < ϕ < 270
    Значит угол ϕ лежит в третьей четверти и его sin ϕ < 0.
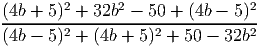
    cos2ϕ + sin2ϕ = 1
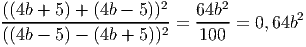
    9 16 sin2 ϕ = 1 - ---= --- 25 25
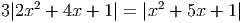
    4 sin ϕ = - -- 5
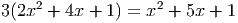
    √ -- cos α = cos(ϕ - 60) = cos ϕ * cos 60 + sin ϕ * sin60 = cosϕ 1+ sin ϕ--3- 2 2
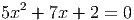
    ( √ -) √ -- 3-- 4--3- 3-+-4--3- cosα = - 10 + 10 = - 10
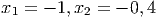
    Ответ: cos α = -3+4√3- 10
  • Найдите площадь треугольника, ограниченного линиями y = x - 2,y = -x - 2,y = 0. Решение: Построим все три прямые и заметим, что они ограничивают треугольник с основанием 4 и высотой 2. По формуле площади треугольника S = 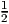1 2 * 2 * 4 = 4 Ответ: S = 4
  • В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60∘. Докажите, что трапеция - равнобедренная.
    Решение: Продолжим AD за точку D на расстояние DM = BC.
    PIC
     
    BC = DE
    BCDE - параллелограмм
    AC = AD + BC = AD + DE = AE
    Значит △ACE равнобедренный, но ∠AOD = ∠ACE = 60, значит треугольник △ACE равносторонний. Тогда ∠CAD = ADB = 60 и треугольник △AOD равносторонний. Очевидно, что и треугольник △BOC равносторонний. Значит диагонали трапеции BD = AC равны между собой. Отсюда треугольники △COD = △BOA равны, значит равны стороны AB и CD. Трапеция равнобедренная.