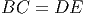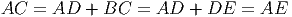Вариант 2.
- По двум параллельным железнодорожным путям в одном направлении следуют товарный и пассажирский поезд, скорости которых равны соответственно 40 км/ч и 100 км/ч. Длина товарного поезда равна 750 м. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда равно 1 минуте.
- Сократите дробь
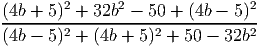
- Решите уравнение
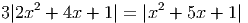
- sin α =
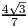 ,
, 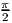 < α < π. Найдите
< α < π. Найдите 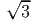 sin 2α + sin
sin 2α + sin 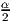
- Найдите площадь треугольника, ограниченного линиями y = x - 3,y = -x + 3,x = 0.
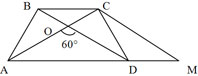
- В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60∘. Докажите, что трапеция - равнобедренная.
- По двум параллельным железнодорожным путям в одном направлении следуют товарный и пассажирский поезд, скорости которых равны соответственно 40 км/ч и 100 км/ч. Длина товарного поезда равна 750 м. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда равно 1 минуте.
Решение: Пусть длина пассажирского поезда l метров. Скорость пассажирского поезда относительно товарного 100 - 40 = 60 км/ч или 1000 м/мин. Пассажирский поезд прошел мимо товарного за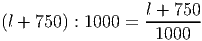
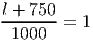
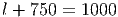
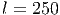
- Сократите дробь
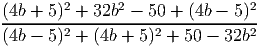
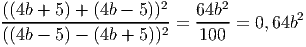
Ответ: 0, 64b2 - Решите уравнение
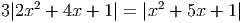
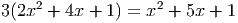
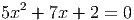
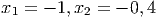
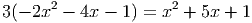
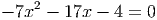
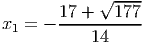
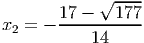
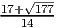 , -
, -
- sin α =
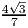 ,
, 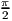 < α < π. Найдите
< α < π. Найдите 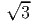 sin 2α + sin
sin 2α + sin 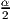
Решение: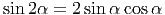
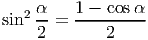
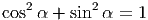
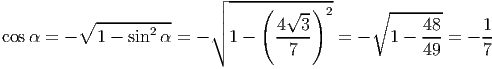
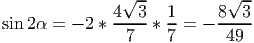
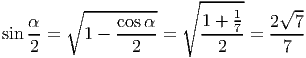
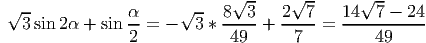
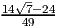
- Найдите площадь треугольника, ограниченного линиями y = x - 3,y = -x + 3,x = 0.
Решение: Построим все три прямые и заметим, что они ограничивают треугольник с основанием 6 и высотой 3. По формуле площади треугольника S =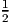 * 3 * 6 = 9 Ответ: S = 9
* 3 * 6 = 9 Ответ: S = 9 - В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60∘. Докажите, что трапеция - равнобедренная.
Решение: Продолжим AD за точку D на расстояние DM = BC.