Упражнения
Упражнение 1
Параллельны ли прямые a и b см. рис, если
- угол 1 равен углу 3;
- угол 1 равен углу 4;
- сумма углов 1 и 2 равна 180∘;
- сумма углов 5 и 6 равна 90∘?
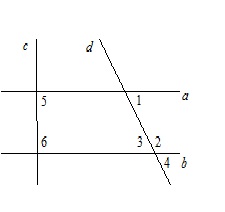
1) 2) 3) Прямые параллельны. 4) Прямые не параллельны.
Упражнение 2
На рис △ABC = △CDE,BC = DE. Докажите, что AB||CD.
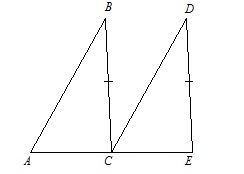
Так как △ABC = △CDE и BC = DE, то углы ∠BAC и ∠DCE равны. Эти углы соответственные, поэтому AB||CD, ч.т.д.
Упражнение 3
На рисунке AB = BC, угол ∠A равен 60∘, CD - биссектриса угла ∠BCE. Докажите, что AB||CD.
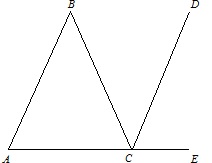
Поскольку AB = BC, треугольник △ABC – равнобедренный, так что угол ∠BCA равен углу ∠A, то есть 60∘. Тогда смежный с ним угол ∠BCE равен 120∘. Так как CD - биссектриса, то углы ∠BCD и ∠DCE равны 60∘. Поэтому соответственные углы ∠BAC и ∠DCE равны, откуда получаем AB||CD, ч.т.д.
Упражнение 4
На рисунке AB = CD и BC = AD. Докажите, что BC||AD.
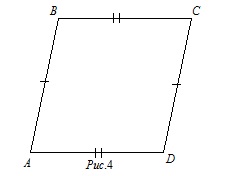
Проведем диагональ BD. Так как AB = CD и AD = BC, а сторона BD - общая, то треугольники △ABD и △CBD равны по трем сторона. Следовательно, равны углы ∠ADB и ∠CBD. Эти углы – накрест лежащие, поэтому BC||AD, ч.т.д.
Упражнение 5
На рисунке угол 1 равен углу 2, BC = EF, AD = CF. Докажите, что AB||DE.
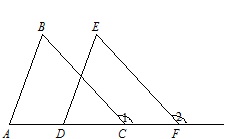
Так как равны углы 1 и 2, то равны и смежные с ними углы ∠ACB и ∠DFE. Поскольку AD = CF, то AC = DF. По условию, BC = EF. Таким образом, △ABC = △DEF по двум сторонам и углу между ними. Тогда угол ∠BAC равен углу ∠EDF. Эти углы соответственные, так что AB||DE, ч.т.д.
Упражнение 6
На рисунке углы ∠ABD и ∠DBC равны, BD⊥AC, AC - биссектриса угла ∠BAE. Докажите, что BC||AE.
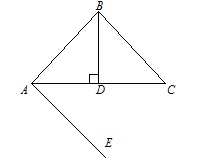
Прямые углы ∠ADB и ∠CDB равны, угол ∠ABD равен углу ∠CBD, BD - общая сторона, значит, △ABD = △BCD по двум углам и стороне между ними. Поэтому угол ∠BCD равен углу ∠BAD. Так как AD - биссектриса, то угол ∠DAE равен углу ∠BAD, а следовательно и углу ∠BCD. Углы ∠DAE и ∠BCD – накрест лежащие, поэтому BC||AE, ч.т.д.
Упражнение 7
На рисунке AM = MD,DE = DF и AE = AF. Докажите, что MD||AF.
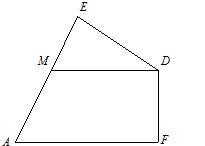
Соединим точки A и D. Тогда △ADE = △ADF по трем сторонам. Поэтому угол ∠DAE равен углу ∠DAF. В равнобедренном треугольнике △AMD угол ∠ADM равен углу ∠DAM, то есть углу ∠DAE. Таким образом, накрест лежащие углы ∠DAF и ∠ADM равны, откуда MD||AF, ч.т.д.
Упражнение 8
Один из внутренних односторонних углов, образованных при пересечении двух параллельных прямых третьей, в 3 раза больше другого. Чему равны эти углы?
Углы равны 45∘ и 135∘.
Упражнение 9
Дан прямоугольный треугольник △ACB (угол ∠C - прямой), E лежит на AC, F лежит на AB, причем EF||CB, EK - биссектриса треугольника △AEF. Чему равен угол ∠AEK
Угол ∠AEK равен 45∘.
Упражнение 10
На рисунке AC||BD и AC = AB, угол ∠MAC равен 40∘. Найдите угол ∠CBD.
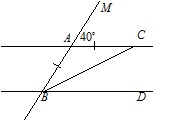
Угол ∠CBD равен 20∘ (равны углы ∠ABC,∠ACB∠CBD).
Упражнение 11
Отрезки CD и AB пересекаются в точке O так, что AO = OB, AC||DB. Докажите, что △AOC = △OB.
Углы ∠AOC и ∠DOB равны как вертикальные. Углы ∠CAO и ∠DBO равны как накрест лежащие, поскольку AC||DB. По условию, AO = OB. Таким образом, △AOC = △DOB по двум углам и стороне между ними, ч.т.д.
Упражнение 12.
На рисунке AB = BD = BC,BE||DC. Докажите, что DC⊥AC.
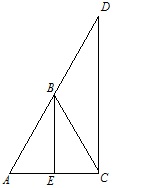
В равнобедренном треугольнике △ABC угол ∠BCA равен углу ∠BAC. В равнобедренном треугольнике △BCD угол ∠BCD равен углу ∠BDC. Угол ∠ACD равен сумме углов ∠BCA и ∠BCD, а следовательно, сумме углов ∠BAC и ∠BDC, то есть сумме углов ∠DAC и ∠ADC. Поскольку сумма углов треугольника △ACD равна 180∘, то угол ∠ACD равен 90∘, то есть DC⊥AC, ч.т.д.
Упражнение 13
На рисунке BE||AF,AB||DE,AB = CD. Докажите, что △BCE = △ADF.
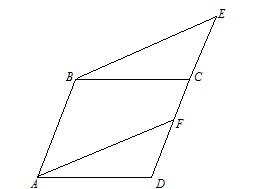
Поскольку BE||AF и AB||EF, то ABEF - параллелограмм. Тогда AF = BE и AB = EF, так как противоположные стороны параллелограмма равны. Далее, CD = AB = EF, поэтому CE = DF. Соответственные углы ∠BEC и ∠AFD равны, потому что BE||AF. Вместе с равенствами BE = AFCE = DF это дает равенство треугольников △BCE и △ADF, ч.т.д.
Упражнение 14
На прямой MN между точками M и N выбрана точка A и проведены по одну сторону от MN лучи AB, AC и AD. На луче AB выбрана точка K и через нее проведена прямая, параллельная MN и пересекающая лучи AC и AD соответственно в точках P и E, KP = PA = PE. Докажите, что AB⊥AD.
Обозначим угол ∠AKP за x, угол ∠AEP за y. Так как KP = PA, то угол ∠KAP тоже равен x. Аналогично, поскольку PE = PA, угол ∠EAP равен y. Угол ∠BAD тогда равен x + y. Прямые KE и MN параллельны, поэтому равны накрест лежащие углы ∠KAM и ∠AKP, а также ∠EAN и ∠AEP, то есть угол ∠KAM равен x, угол ∠EAN равен y. Угол ∠MAN – развернутый, следовательно 2x + 2y = 180∘. Тогда x + y = 90∘, откуда получаем, что AB⊥AD, ч.т.д.
Упражнение 15
Используя данные на рисунке, найдите углы 1, 2 и 3.
Угол 1 равен 50∘. Угол 2 равен 130∘. Угол 3 равен 50∘.
Упражнение 16
На рис.12 A1B1||AB,A1K1 - биссектриса угла ∠MA1B1,AK - биссектриса угла ∠MAB. Докажите, что угол ∠MA1K1 равен углу ∠MAK. Могут ли пересекаться прямые A1K1 и AK?
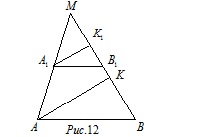
Так как A1B1||AB, то соответственные углы ∠MA1B1 и ∠MAB равны. Угол ∠MA1K1 равен половине угла ∠MA1B1, так как A1K1 - биссектриса. Также угол ∠MAK равен половине угла ∠MAB, поскольку AK - биссектриса. Таким образом, углы ∠MA1K1 и ∠MAK равны, ч.т.д. Прямые A1K1 и AK не могут пересекаться: они параллельны, поскольку равны соответственные углы ∠MA1K1 и ∠MAK.
Упражнение 17
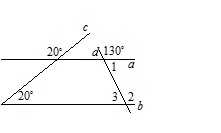
Один из углов, образованных при пересечении прямой d прямыми a и b, равен 50∘ (см. рисунок). Может ли один из остальных семи углов равняться 20∘? Почему?

Ни один из остальных семи углов при пересечении прямой d прямыми a и b не может равняться 20∘. Согласно свойствам накрест лежащих, односторонних и соответственных углов, все они равны либо 50∘, либо 130∘.
Упражнение 18
На рис.14 BA||DE. Докажите, что угол ∠BCD равен сумме углов ∠B и ∠D.
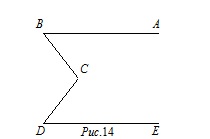
Проведем через точку C прямую CF, параллельную BA. Накрест лежащие углы ∠ABC и ∠BCF равны. Так как BA||DE, то CF||DE. Тогда равны накрест лежащие углы ∠CDE и ∠DCF. Угол ∠BCD равен сумме углов ∠BCF и ∠DCF, а следовательно, сумме углов ∠B и ∠D, ч.т.д.
Упражнение 19
На рис.15 угол ∠BED равен 70∘, угол ∠EDC равен 20∘, AB||CD. Найдите угол ∠ABC.
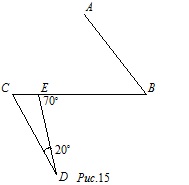
Угол ∠ABC равен 50∘.
Упражнение 20
Внутри треугольника △ABC отмечена точка F. Через нее проведены прямые, параллельные сторонам AB и AC и пересекающие сторону BC соответственно в точках M и E,FM = BM,FE = CE. Докажите, что F - точка пересечения биссектрис треугольника △ABC.
В равнобедренном треугольнике △BFM угол ∠FBM равен углу ∠BFM. Так как прямые FM и AB параллельны, накрест лежащие углы ∠ABF и ∠BFM равны. Таким образом, равны углы ∠ABF и ∠FBM, следовательно, BF - биссектриса угла ∠ABC. Аналогично, поскольку треугольник △CEF - равнобедренный, а прямые AC и EF параллельны, то CF - биссектриса угла ∠ACB. Две биссектрисы треугольника △ABC проходят через точку F, поэтому она и есть точка пересечения биссектрис, ч.т.д.
Упражнение 21
На рисунке BD - медиана треугольника △ABC, причем AB = 2BD. Докажите, что BC - биссектриса угла ∠DBF.
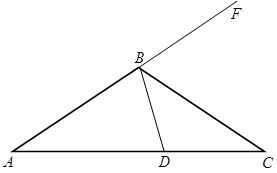
Продлим медиану BD на ее длину до точки E. AB = 2BD = BE, и в равнобедренном треугольнике △ABE равны углы ∠BAE и ∠AEB. Так как AD = CD,BD = DE и вертикальные углы ∠ADE и ∠BDC равны, то △BCD = △ADE. Тогда углы ∠AED и ∠CBD равны, а следовательно, BC||AE. Таким образом, равны соответственные углы ∠CBF и ∠BAE. Последний равен углу ∠AEB, то есть ∠AED, который равен углу ∠CBD. Получаем, что углы ∠CBF и ∠CBD равны. Это и означает, что BC - биссектриса угла ∠DBF, ч.т.д.

















