Задачи
Задача 1. В остроугольном треугольнике ABC окружность с диаметром BC пересекает высоту AD в точке M. Высоты треугольника пересекаются в точке H. Найдите AH, если AD = 32 и DM = 8.
Задача 1, решение. Проведем отрезки BM и CM. Угол BMC вписан в окружность и опирается на ее диаметр BC, так что ∠BMC = 90∘, по теореме о вписанном угле.
Тогда △BMC прямоугольный и MD – его высота, проведенная к гипотенузе. Здесь возникает 3 подобных прямоугольных треугольника: △BMC, △BMD и △CMD. Из этого подобия следует, что DM2 = BD ⋅ CD. Так как по условию DM = 8, то BD ⋅ CD = 64.
В треугольнике ABC проведем высоты BE и CF, которые пересекут AD в точке H. И обозначим как β угол B. Поскольку △ABD прямоугольный, то 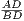 = tg β. △BCF тоже прямоугольный, поэтому ∠BCF = 90∘- β. Наконец, △CDH прямоугольный, и в нем ∠DCH = 90∘-β (очевидно, ∠DCH = ∠BCF). Тогда ∠CHD = β и
= tg β. △BCF тоже прямоугольный, поэтому ∠BCF = 90∘- β. Наконец, △CDH прямоугольный, и в нем ∠DCH = 90∘-β (очевидно, ∠DCH = ∠BCF). Тогда ∠CHD = β и 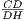 = tg β.
= tg β.
Получаем 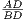 = tg β =
= tg β =  , откуда AD ⋅ DH = BD ⋅ CD. Но мы знаем, что BD ⋅ CD = 64 и по условию AD = 32. Тогда DH = 64∕32 = 2 и AH = AD - DH = 30.
, откуда AD ⋅ DH = BD ⋅ CD. Но мы знаем, что BD ⋅ CD = 64 и по условию AD = 32. Тогда DH = 64∕32 = 2 и AH = AD - DH = 30.
Ответ. AH = 30
Комментарий. Начало решения – пример того, как можно использовать имеющуюся в условии задачи окружность, через вписанные в нее углы.
Упомянутое подобие трех прямоугольных треугольников и следствия из него подробно разобраны в учебнике геометрии 7-9 класса, в разделе «пропорциональные отрезки в прямоугольном треугольнике».
При проведении высот в треугольнике возникают многочисленные прямоугольные треугольники. Их углы можно выразить через углы исходного треугольника. Точнее, у каждого из прямоугольных треугольников один из острых углов равен одному из углов исходного треугольника (если исходный – остроугольный).
Задача 2. Окружность радиуса 8 касается основания AC равнобедренного треугольника ABC и продолжений его боковых сторон. Найдите радиус вписанной окружности треугольника ABC, если AC = 12.
Задача 2, решение. Обозначим O центр указанной окружности, K и L – точки ее касания с продолжениями сторон AB и BC соответственно. Обозначим M середину основания AC. Докажем, что окружность касается AC в точке M.
Радиус окружности в точке касания перпендикулярен касательной, поэтому OK ⊥ AB и OL ⊥ BC. Тогда расстояния от O до прямых AB и BC равны OK и OL, они оба равны радиусу и равны 8. Это значит, что точка O лежит на биссектрисе угла ABC. Но в равнобедренном △ABC биссектриса угла ABC совпадает с медианой BM, а также является высотой (нам потом потребуется, что BM ⊥ AC). Таким образом, O лежит на прямой BM и OM ⊥ AC. Наконец, если окружность касается AC в какой-то точке N, то ON ⊥ AC, откуда прямые OM и ON совпадают, а следовательно, совпадают и сами точки M и N, ч.т.д.
Рассмотрим △ABM и △BOK. Они оба прямоугольные (∠AMB = ∠OKB = 90∘) и имеют одинаковый острый угол при вершине B. Значит, треугольники подобны, откуда
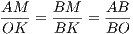
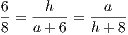
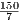 = 21
= 21 , h =
, h = 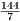 = 20
= 20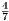 .
.
Теперь, зная стороны и высоту △ABC, можно найти радиус его вписанной окружности. Воспользуемся формулой S = p ⋅ r, где S – площадь, p = P∕2 – полупериметр, r – радиус вписанной окружности. В данном случае S = 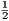 AC ⋅ BH = 6BH = 6h =
AC ⋅ BH = 6BH = 6h = 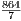 . Периметр P = AB + BC + AC = 2AB + AC = 2a + 12, полупериметр p =
. Периметр P = AB + BC + AC = 2AB + AC = 2a + 12, полупериметр p = 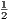 P = a + 6 =
P = a + 6 = 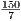 + 6 =
+ 6 = 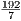 . Так что r =
. Так что r = 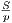 =
= 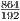 = 4,5.
= 4,5.
Ответ. Радиус вписанной окружности равен 4,5.
Комментарий. Указанная в условии окружность (та, которая радиуса 8) называется «вневписанная окружность треугольника».
Из симметрии картинки кажется, что окружность должна касаться AC именно в точке M.
Точка, лежащая внутри угла, равноудалена от сторон угла тогда и только тогда, когда она лежит на биссектрисе – см. учебник геометрии 7-9 класс, раздел «свойства биссектрисы угла и срединного перпендикуляра к отрезку».
Отрезки касательных к окружности, проведенные из одной точки, равны – см. учебник геометрии 7-9 класс, раздел «касательная к окружности».
Перемножение пропорций «крест-накрест» – известный прием из школьного курса алгебры. Равенство 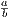 =
= 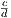 после домножения на произведение знаменателей bd превращается в ad = bc.
после домножения на произведение знаменателей bd превращается в ad = bc.
Формула S = p ⋅ r верна не только для треугольника, но для любого многоугольника, в который можно вписать окружность. Многоугольник можно разбить на треугольные сектора, соединяя центр вписанной окружности со всеми вершинами. Площадь каждого сектора – половина произведения соответствующей стороны на радиус окружности (радиус будет высотой треугольника).
Задача 3. В выпуклом четырехугольнике ABCD точка O – середина диагонали BD. Длина диагонали AC равна 50. Расстояния от точки O до всех сторон четырехугольника равны 7. Найдите площадь четырехугольника.
Задача 3, решение. Так как точка O равноудалена от сторон AB и BC, то она лежит на биссектрисе угла B. Поскольку O лежит на диагонали BD, то BD – биссектриса угла B (∠ABD = ∠CBD). Также точка O равноудалена от сторон AD и CD. Аналогично, BD – биссектриса угла D (∠ADB = ∠CDB).
Получаем, что △ABD = △BCD (сторона BD общая, углы при вершине B равны, углы при вершине D тоже равны). Отсюда AB = BC и AD = CD.
Далее, точка O равноудалена от сторон AB и AD, поэтому она лежит на биссектриса угла A. В треугольнике ABD отрезок AO будет не только биссектрисой, но и медианой. Тогда △ABD равнобедренный, AB = AD. Наконец, в четырехугольнике ABCD все стороны равны (BC = AB, AB = AD, AD = CD) и поэтому ABCD – ромб.
В ромбе ABCD точка O будет точкой пересечения диагоналей AC и BD, так как диагонали ромба (и любого параллелограмма) точкой пересечения делят друг друга пополам. Отсюда же AO = CO = AC∕2 = 25. Кроме того, диагонали ромба перпендикулярны, так что ∠AOB будет прямым (а △AOB прямоугольным).
Опустим из точки O перпендикуляр OH на сторону AB. Получим прямоугольный △AOH. В нем OH = 7, как расстояние от O до стороны AB, и AO = 25 (см. выше). По теореме Пифагора можно найти, что AH = 24.
Прямоугольные треугольники AOB и AOH имеют общий острый угол при вершине A. Обозначим этот угол α. Тогда tg α =  и tg α =
и tg α = 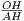 . Таким образом,
. Таким образом,  =
= 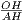 ,
, 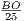 =
= 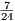 и BO =
и BO = 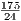 .
.
Найдем площадь ромба ABCD как половину произведения диагоналей. AC = 50 по условию, BD = 2BO = 2 ⋅ =
= 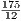 . Так что SABCD =
. Так что SABCD = 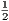 ⋅ AC ⋅ BD =
⋅ AC ⋅ BD =  ⋅ 50 ⋅
⋅ 50 ⋅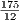 =
= 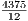 = 364
= 364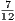 .
.
Ответ. Площади ромба равна 364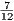 .
.
Комментарий. Точка, лежащая внутри угла, равноудалена от сторон угла тогда и только тогда, когда она лежит на биссектрисе – см. учебник геометрии 7-9 класс, раздел «свойства биссектрисы угла и срединного перпендикуляра к отрезку».
В равнобедренном треугольнике биссектриса, высота и медиана к основанию совпадают. Верна и обратная теорема: достаточно совпадения медианы с высотой, высоты с биссектрисой или биссектрисы с медианой, чтобы треугольник был равнобедренным.
Если все стороны четырехугольника равны, то это ромб. Действительно, если все стороны равны, то противоположные стороны попарно равны – и этого достаточно, чтобы четырехугольник был параллелограммом (см. признаки параллелограмма в учебнике геометрии 7-9 класс). А если в параллелограмме все стороны равны, то это ромб по определению.
Можно было, вместо равенства с тангенсом, заметить, что OH – высота в прямоугольном △AOB и воспользоваться возникающим при этом подобием трех треугольников, как это было в решении задачи 1.
В конце можно было вычислить площадь по-другому: найти SAOB = 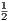 ⋅AO⋅BO, далее заметить равенство 4х треугольников (AOB, BOC, COD и AOD) и получить SABCD = 4SAOB. Фактически, это воспроизводит доказательство формулы «площадь ромба равна половине произведения диагоналей».
⋅AO⋅BO, далее заметить равенство 4х треугольников (AOB, BOC, COD и AOD) и получить SABCD = 4SAOB. Фактически, это воспроизводит доказательство формулы «площадь ромба равна половине произведения диагоналей».
Задача 4. В треугольника ABC биссектриса AP и медиана BM пересекаются в точке K. Отношение AC : AB = 5 : 7. Найдите отношение площадей SKPCM : SABC.
Задача 4, решение. Так как AP – биссектриса, то CP : BP = AB : AC = 5 : 7 (там отношение 5:7 по условию). Также SACP : SABP = CP : BP, значит SACP : SABP = 5 : 7, поэтому 7SACP = 5SABP.
Так как AP – биссектриса треугольника ABC, то и отрезок AK – биссектриса треугольника ABM. Отсюда KM : BK = AM : AB. Также SAKM : SABK = KM : BK. Поскольку BM – медиана, AM = AC∕2 и AM : AB = 2AM : 2AB = AC : 2AB = 5 : 14. Тогда SAKM : SABK = 5 : 14 и можно ввести такую величину x, что SAKM = 5x, SABK = 14x.
Далее, SABM = SABK + SAKM = 14x + 5x = 19x. Опять же, BM – медиана, так что SABM : SBCM = AM : CM = 1 : 1. Отсюда SBCM = SABM = 19x и SABC = SABM + SBCM = 19x + 19x = 38x. Обозначим SKPCM = y. Тогда SBKP = SBCM - SKPCM = 19x - y.
Теперь SACP = SAKM+SKPCM = 5x+y и SABP = SABK+SBKP = 14x+19x-y = 33x-y. Вспомним про 7SACP = 5SABP и получим 7 ⋅ (5x + y) = 5 ⋅ (33x - y), 35x + 7y = 165x - 5y и 130x = 12y.
Наконец, посчитаем отношение SKPCM : SABC.
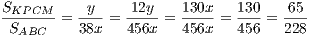
(Использовали то, что SABC = 38x, SKPCM = y и 130x = 12y.)
Ответ. SKPCM : SABC = 65 : 228.
Комментарий. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Подробности можно найти в учебнике геометрии 7-9 класса, среди задач после раздела «отношение площадей подобных треугольников».
У треугольников с общей высотой отношению площадей равно отношению оснований (так как площадь – половина произведения высоты на основание). В нашей задаче это свойство используется для трех пар треугольников: △ABP и △ACP, △ABK и △AMK, △ABM и △BCM.
Для медианы есть отдельное свойство, что медиана делит треугольник на два равновеликих треугольника. Действительно, у этих двух треугольников основания равны (в 2 раза меньше, чем у исходного треугольника), а высота общая.
Задача 5. В треугольнике ABC медиана AD и биссектриса BE перпендикулярны и равны 64. Найдите стороны треугольника.
Задача 5, решение. Обозначим P точку пересечения AD и BE. В треугольнике ABD отрезок BP является биссектрисой (BP – биссектриса угла B) и высотой (BP ⊥ AD). Тогда △ABD равнобедренный, AB = BD. Также BP является медианой, отсюда AP = DP = AD∕2 = 32.
Опустим из точки C перпендикуляр CQ на прямую BP (куда-то на ее продолжение за точку E). Получим прямоугольный △BCQ. Он имеет общий острый угол при вершине B с прямоугольным △BDP, так что эти два треугольника подобны. Из подобия получаем:
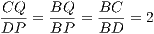
Рассмотрим еще одну пару прямоугольных треугольников: △AEP и △CEQ. У них равны острые углы при вершине E (они вертикальные), поэтому треугольники подобны. Из этого подобия:
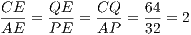
Теперь мы знаем в прямоугольном △BDP два катета: DP = 32 и BP = 48. По теореме Пифагора, BD = 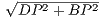 =
=  = 16
= 16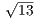 . Отсюда AB = BD = 16
. Отсюда AB = BD = 16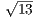 и BC = 2BD = 32
и BC = 2BD = 32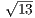 .
.
Наконец, вычислим сторону AC. В прямоугольном △AEP известны катеты: AP = 32, PE = 16. По теореме Пифагора, AE =  =
= 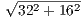 = 16
= 16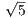 . Также CE = 2AE, откуда AC = AE + CE = 3AE = 3 ⋅ 16
. Также CE = 2AE, откуда AC = AE + CE = 3AE = 3 ⋅ 16 = 48
= 48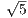 .
.
Ответ. AB = 16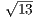 , BC = 32
, BC = 32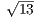 и AC = 48
и AC = 48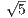 .
.
Комментарий. В равнобедренном треугольнике биссектриса, высота и медиана к основанию совпадают. Верна и обратная теорема: достаточно совпадения медианы с высотой, высоты с биссектрисой или биссектрисы с медианой, чтобы треугольник был равнобедренным.
Для подобия прямоугольных треугольников достаточно равенства одного острого угла. Прямые углы образуют вторую пару равных углов, а по двум равным углам треугольники подобны, это стандартный признак.
Когда у нас есть несколько величин, связанных известными соотношениями, стандартный прием – как-то обозначить одну из них (лучше самую маленькую) и выразить через нее все остальные.
Задача 6. Диагонали трапеции равны 15 и 7, средняя линия равна 10. Найдите площадь трапеции.
Задача 6, решение. Обозначим трапецию ABCD (BC и AD – основания, AB и CD – боковые стороны). Пусть AC = 7, BD = 15 (диагонали равны 7 и 15 по условию). Проведем в трапеции высоты BH и CK к стороне AD, обозначим длину высот как h. Образуется прямоугольник BCKH, обозначим длину его сторон BC и HK как a. Наконец, обозначим AH = x и DK = y.
Треугольник ACK прямоугольный, его гипотенуза AC = 7, катеты AK = HK + AH = a + x и CK = h. По теореме Пифагора, (a + x)2 + h2 = 49. Треугольник BDH тоже прямоугольный, гипотенуза BD = 15, катеты DH = HK + DK = a + y и BH = h. Опять же, по теореме Пифагора, (a + y)2 + h2 = 225. Вычитая два полученных равенства, имеем (a + y)2 - (a + x)2 = 225 - 49 и далее (2a + x + y)(y - x) = 176.
Так как средняя линия трапеции, по условию, равна 10, то сумма оснований AD + BC = 20. С другой стороны, BC = a и AD = AH + HK + DK = x + a + y, так что AD + BC = 2a + x + y. Поэтому 2a + x + y = 20. Подставим в равенство (2a + x + y)(y - x) = 176 и получим y - x = 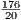 = 8,8.
= 8,8.
Вернемся к 2a + x + y = 20, подставим y = x + 8,8. Тогда 2a + 2x + 8,8 = 20 и a + x = 5,6. Наконец, вспомним равенство (a + x)2 + h2 = 49, из него следует h2 = 49 - (a + x)2 = 49 - 5,62 = 17,64, откуда h = 4,2.
Наконец, поскольку средняя линия трапеции равна 10, то SABCD = 10 ⋅ h = 10 ⋅ 4,2 = 42.
Ответ. Площадь трапеции равна 42.
Комментарий. Средняя линия трапеции равна полусумме оснований. И площадь трапеции равна не только произведению полусуммы оснований на высоту, но и произведению средней линии на высоту.
В целом решение скорее алгебраическое, чем геометрическое. Так тоже можно, когда неизвестных мало, или взаимосвязей между ними много.
Задача 7. В треугольнике ABC сторона AB = 16, ∠C = 105∘, AK и BM – высоты, точка P – середина стороны AB. Найдите площадь треугольника MPK.
Задача 7, решение. По условию, ∠ACB = 105∘. Треугольник ABC – тупоугольный, так что высоты AK и BM опущены на продолжения сторон BC и AC. Углы ACK и BCM в таком случае смежные с углом ACB и равны 180∘- 105∘ = 75∘. Треугольники ACK и BCM прямоугольные. В △ACK угол AKC прямой, ∠ACK = 75∘ и тогда ∠CAK = 15∘. Аналогично, в △BCM угол BMC прямой, ∠BCM = 75∘ и тогда ∠CBM = 15∘.
Обозначим в треугольнике ABC угол A как α, угол B как β. Тогда ∠KAB = α + 15∘, ∠ABM = β + 15∘. Рассмотрим прямоугольные треугольники AKB и AMB, в них AB – гипотенуза, P – середина гипотенузы, а KP и MP – медианы, проведенные к гипотенузе. Такая медиана равна половине гипотенузы, так что KP = MP = AB∕2 = 8. Также AP = BP = AB∕2 = 8. Итого, треугольники AKP и BMP равнобедренные.
Рассмотрим равнобедренный △AKP. В нем AP = KP = 8 и ∠KAP = α + 15∘. Поэтому ∠AKP = ∠KAP = α + 15∘, и далее ∠APK = 150∘- 2α. Аналогично в равнобедренном △BMP получим ∠BPM = 150∘- 2β. Три угла APK, BPM и KPM – смежные, их сумма равна 180∘. Используя выражения для ∠APK и ∠BPM, найдем что ∠KPM = 2α + 2β - 120∘.
В исходном треугольнике ABC сумма углов тоже равна 180∘, так что α + β + 105∘ = 180∘. Следовательно, α + β = 75∘. Тогда 2α + 2β = 150∘ и 2α + 2β - 120∘ = 30∘, то есть ∠KPM = 30∘.
Наконец, вычислим площадь треугольника MPK: SMPK =  ⋅ KP ⋅ MP ⋅ sin∠KPM =
⋅ KP ⋅ MP ⋅ sin∠KPM = 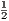 ⋅ 8 ⋅ 8 ⋅ sin30∘ = 32sin30∘ = 32 ⋅
⋅ 8 ⋅ 8 ⋅ sin30∘ = 32sin30∘ = 32 ⋅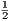 = 16.
= 16.
Ответ. Площадь треугольника MPK равна 16.
Комментарий. Зная два угла треугольника, мы всегда можем найти третий, так как сумма трех углов равна 180∘.
Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы и делит этот треугольник на два равнобедренных треугольника. Заодно, середина гипотенузы будет центром описанной окружности исходного треугольника.
Последнее свойство проще всего доказать так. Пусть XY Z – прямоугольный треугольник с прямым углом Z. Отметим на гипотенузе такую точку T, что ∠XZT = ∠ZXY . Тогда △XZT будет равнобедренным, а именно XT = ZT. Далее, ∠Y ZT = 90∘-∠XZT = 90∘-∠ZXY = ∠XY Z. Отсюда △Y ZT тоже будет равнобедренным, то есть Y T = ZT. Из тройного равенства XT = ZT = Y T следует, что T – середина гипотенузы XY , а ZT – медиана. Из этого же равенства следует, что медиана ZT равна половине гипотенузы XY и что точка T будет центром описанной окружности треугольника XY Z.
В целом, решение основано на вычислении углов, местами более «алгебраическое», чем «геометрическое».
Задача 8. В параллелограмме ABCD стороны AB = 2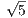 , BC = 5
, BC = 5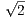 . M – середина стороны AD и отрезок BM перпендикулярен диагонали AC. Найдите длину диагонали BD.
. M – середина стороны AD и отрезок BM перпендикулярен диагонали AC. Найдите длину диагонали BD.
Задача 8, решение. Обозначим как O точку пересечения диагоналей AC и BD. Поскольку диагонали параллелограмма точкой пересечения делятся пополам, O будет серединой BD. В треугольнике ABD отрезки BM и AO будут медианами. Обозначим как P точку пересечения этих медиан. Также обозначим PO = x, PM = y. Так как медианы треугольника делятся точкой пересечения в отношении 2:1, то AP = 2x и BP = 2y.
По условию, BM ⊥ AC, то есть AO ⊥ BM. При их пересечении образуются прямоугольные треугольники APB, APM и BPO. По теореме Пифагора для △APB: AP2 + BP2 = AB2, (2x)2 + (2y)2 = (2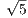 )2 и 4x2 + 4y2 = 20. По теореме Пифагора для △APM: AP2 + PM2 = AM2 и 4x2 + y2 = AM2. Так как M – середина AD, то AM =
)2 и 4x2 + 4y2 = 20. По теореме Пифагора для △APM: AP2 + PM2 = AM2 и 4x2 + y2 = AM2. Так как M – середина AD, то AM = 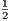 AD и AM2 =
AD и AM2 = 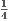 AD2. Далее, AD = BC = 5
AD2. Далее, AD = BC = 5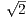 , поскольку противоположные стороны параллелограмма равны и BC = 5
, поскольку противоположные стороны параллелограмма равны и BC = 5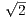 по условию. Отсюда AD2 = (5
по условию. Отсюда AD2 = (5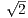 )2 = 50 и AM2 =
)2 = 50 и AM2 = 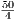 = 12.5. Наконец, 4x2 + y2 = 12.5.
= 12.5. Наконец, 4x2 + y2 = 12.5.
Вычтем из равенства 4x2 + 4y2 = 20 равенство 4x2 + y2 = 12.5, получим 3y2 = 7.5 и y2 = 2.5. Поэтому 4x2 = 20 - 4x2 = 20 - 4 ⋅ 2.5 = 10 и x2 = 2.5. Наконец, по теореме Пифагора для △BPO: BP2 + PO2 = BO2, 4y2 + x2 = BO2 и BO2 = 4 ⋅ 2.5 + 2.5 = 12.5. Так как O – середина BD, то BD = 2BO и BD2 = 4BO2 = 4 ⋅ 12.5 = 50. Наконец, BD = 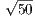 = 5
= 5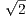 .
.
Ответ. BD = 5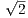 .
.
Комментарий. Аналогично ряду других задач, решение скорее «алгебраическое». Данная в условие перпендикулярность используется через теорему Пифагора. Условие про середину стороны используется для построения медианы и дальнейшего применения теоремы о пересечении медиан.
Задача 9. В трапеции ABCD основания BC = 24 и AD = 32, боковая сторона AB = 7, ∠A + ∠D = 90∘. Найдите радиус окружности, которая проходит через точки A и B и касается прямой CD.
Задача 9, решение. Обозначим центр искомой окружности как O, радиус как R. По условию A и B лежат на окружности, так что AO = BO = R. Тогда точка O лежит на серединном перпендикуляре к отрезку AB. Если обозначить середину AB как M, то прямая OM будет этим серединным перпендикуляром, OM ⊥ AB.
Обозначим как K точку касания искомой окружности и прямой CD. Поскольку касательная к окружности и радиус в точке касания перпендикулярны, то OK ⊥ CD. Также OK = R.
Обозначим как P точку пересечения продолжений сторон AB и CD. В треугольнике ADP тогда ∠A + ∠D = 90∘ (эти углы совпадают с соответствующими углами трапеции). Таким образом, ∠APD = 90∘ и AB ⊥ CD.
Рассмотрим четырехугольник OMPK. Его сторона MP лежит на прямой AB, а сторона PK – на прямой CD. Из OM ⊥ AB следует OM ⊥ MP и ∠OMP = 90∘. Из AB ⊥ CD следует MP ⊥ PK и ∠MPK = 90∘. Также из OK ⊥ CD следует OK ⊥ PK и ∠OKP = 90∘. Так как три угла прямые, OMPK – прямоугольник. В прямоугольнике OMPK (как и в любом параллелограмме) противоположные стороны равны, так что MP = OK = R.
Треугольники BPC и APD имеют общий угол при вершине P. Кроме того, у них равные углы BCP и ADP (соответственные углы при пересечении параллельных прямых BC и AD секущей CD). Значит, △BPC и △APD подобны. Из этого подобия
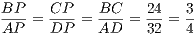
Наконец, поскольку M – середина AB, то BM = AB∕2 = 3.5. Следовательно, MP = BM + BP = 3.5 + 21 = 24.5. Так как R = MP (см. выше), то R = 24.5.
Ответ. Радиус окружности равен 24.5.
Комментарий. Точка равноудалена от концов отрезка тогда и только тогда, когда она лежит на серединном перпендикуляре к этому отрезку. См. учебник геометрии 7-9 класса, раздел «свойства биссектрисы угла и серединного перпендикуляра к отрезку».
Почему если в четырехугольнике три угла прямые, то это прямоугольник? Во-первых, сумма углов четырехугольника равна 360∘, так что четвертый угол тоже пряиой. Далее, если все углы прямые, то сумма любых двух соседних углов равна 180∘. Из этого следует, что каждая пара противоположных сторон параллельна: при пересечении их секущей (третьей стороной) сумма односторонних углов равна 180∘. Тогда наш четырехугольник – параллелограмм по определению. А параллелограмм, в котором все углы прямые – это прямоугольник.
Задача 10. Две окружности, радиусом 6 и 24, касаются друг друга внешним образом к точке K и касаются сторон угла с вершиной A. Общая касательная к окружностям в точке K пересекает стороны угла в точках B и C. Найдите радиус описанной окружности треугольника ABC.
Задача 10, решение. Обозначим центр меньшей окружности как O1, центр большей окружности как O2. Так как каждая окружность касается сторон угла BAC, то O1 и O2 лежат на биссектрисе этого угла. Прямая O1O2 совпадает с биссектрисой угла BAC. Точка K касания окружностей лежит на прямой O1O2, так что она тоже находится на этой биссектрисе.
Обозначим M и N точки касания меньшей и большей окружности соответственно с прямой AB. Так как радиус в точке касания перпендикулярен касательной, то O1M ⊥ AB и O2N ⊥ AB, то есть O1M ⊥ AM и O2N ⊥ AN. Образовавшиеся треугольники AMO1 и ANO2 будут прямоугольными. Эти треугольники подобны, потому что у них есть общий острый угол при вершине A. Из подобия 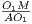 =
= 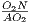 , так что O1M ⋅ AO2 = AO1 ⋅ O2N.
, так что O1M ⋅ AO2 = AO1 ⋅ O2N.
В последнем равенстве обозначим AO1 = a. Тогда AO2 = AO1 + O1O2 = AO1 + O1K + O2K = a + 6 + 24 = a + 30. Кроме того, O1M = 6 и O2N = 24 (используем радиусы окружностей, которые даны в условии). Получаем 6(a + 30) = 24a, откуда 6a + 180 = 24a, 180 = 18a и a = 10, то есть AO1 = 10.
В прямоугольом треугольнике AMO1 катет O1M = 6 и гипотенуза AO1 = 10. По теореме Пифагора можно найти AM = 8. Далее, рассмотрим △AKB – он тоже прямоугольный: радиус O1K лежит на прямой AK и перпендикулярен касательной BC, на которой лежит отрезок BK.
Прямоугольные треугольники AMO1 и AKB подобны, поскольку у них есть общий острый угол при вершине A. Из подобия 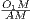 =
= 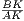 , так что O1M ⋅ AK = BK ⋅ AM. В последнем равенстве O1M = 6, AM = 8, AK = AO1 + O1K = 10 + 6 = 16. Тогда 6 ⋅ 16 = BK ⋅ 8, 8BK = 96 и BK = 12.
, так что O1M ⋅ AK = BK ⋅ AM. В последнем равенстве O1M = 6, AM = 8, AK = AO1 + O1K = 10 + 6 = 16. Тогда 6 ⋅ 16 = BK ⋅ 8, 8BK = 96 и BK = 12.
В треугольнике ABC отрезок AK является биссектрисой и высотой (см. выше: K лежит на биссектрисе угла A и AK ⊥ BC). Значит, этот треугольник равнобедренный, и центр его описанной окружности лежит на луче AK. Обозначим этот центр O3, а радиус этой окружности R. Заметим, что O3A = O3B = R. Также KO3 = AK - AO3 = 16 - R (или KO3 = AO3 -AK = R - 16. Наконец, треугольник BKO3 прямоугольный, и по теореме Пифагора BO32 = KO32 + BK2, то есть R2 = (16 - R)2 + 122.
Из последнего равенства R2 = 256 - 32R + R2 + 144, 32R = 256 + 144 = 400 и R = 12.5.
Ответ. Радиус описанной окружности △ABC равен 12.5.
Комментарий. Расстояние от центра окружности до касательной равно радиусу. Поэтому, если окружность касается двух сторон угла, то расстояния от центра до этих сторон равны радиусу и равны между собой. Кроме того, точка, лежащая внутри угла, равноудалена от сторон угла тогда и только тогда, когда она лежит на биссектрисе – см. учебник геометрии 7-9 класс, раздел «свойства биссектрисы угла и срединного перпендикуляра к отрезку». Следовательно, центр указанной окружности лежит на биссектрисе угла.
Точка касания окружностей лежит на одной прямой с их центрами. От противного: если это не так, то центры и точка касания образуют треугольник. Сумма двух его сторон, равных радиусам окружностей, должна быть больше третьей стороны, равной расстоянию между центрами. Но у окружностей, касающихся внешним образом, сумма радиусов равна расстоянию между центрами. Получаем противоречие, ч.т.д.
Для подобия прямоугольных треугольников достаточно равенства одного острого угла. Прямые углы образуют вторую пару равных углов, а по двум равным углам треугольники подобны, это стандартный признак.
Где лежит центр описанной окружности равнобедренного треугольника? Как у любого треугольника – в точке пересечения серединных перпендикуляров к сторонам. В частности, он лежит на серединном перпендикуляре к основанию. Но этот серединный перпендикуляр – прямая, содержащая биссектрису/медиану/высоту к основанию. Значит, на этой прямой и лежит центр.

















