Задача 1. Решите уравнение:

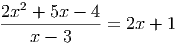
Решение. Домножим на знаменатель и упростим:

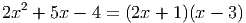
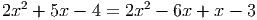
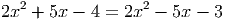
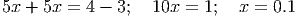
При x = 0.1, x - 3 = 0.1 - 3 = -2.9≠0, это решение подходит.

Ответ.x = 0.1.

Комментарий. Все квадраты неизвестного сокращаются, и уравнение из квадратного становится линейным.
В любом случае, важно проверить, что для найденного решения знаменатель дроби (в исходном уравнении) не равен нулю.

Задача 2. Решите систему неравенств:

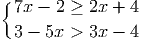
Решение.

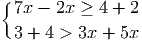
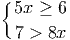
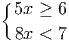
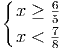
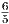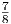> (например, потому что 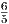> 1, а 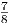< 1).

Изобразим решения неравенств на числовой оси (желтый и синий цвет соответственно).

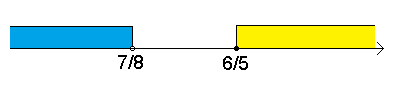
Эти решения не пересекаются.

Ответ. нет решений.

Комментарий. После упрощения остается система из двух неравенств, направленных «в разные стороны». Здесь мы имеем дело с редким случаем, когда решения этих неравенств не пересекаются (обычно в пересечении появляется некий промежуток).

Задача 3. Упростите выражение и найдите его значение при k = 5, m = и n = -1:

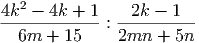
Решение.

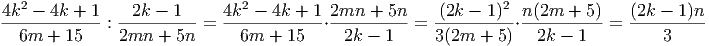
При k = 5 и n = -1:

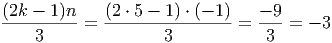
Комментарий. Деление дробей сразу преобразуем в умножение. У первой дроби в числителе можно заметить квадрат разности, в знаменателе вынести 3 за скобку. В числителе второй дроби можно вынести за скобку n. Наконец, умножая дроби, можно сократить 2k - 1 и еще 2m + 5.

Задача 4. Найдите площадь изображенной на рисунке фигуры.

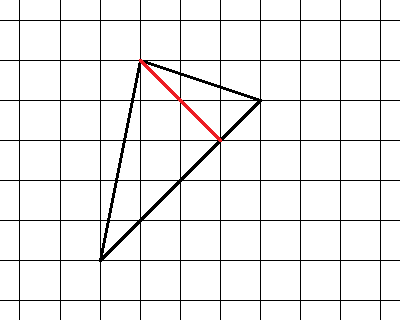
Решение. Площадь треугольника S = ah.
Основание a = 4 («нижняя правая» сторона).
Высота h = 2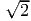 (красная линия из «верхней левой» вершины).

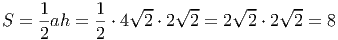
Комментарий. Здесь нет удобной стороны, идущей по линиям сетки (горизонтально или вертикально). Но есть неплохой вариант - сторона, идущая под углом 45^∘ к линиям сетки. Она пересекает 4 клетки по диагонали, а диагональ клетки равна 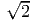. Высота к этой стороне тоже идет под углом 45^∘ к линиям сетки.

Задача 5. В квартиру, где живут два кота, привезли новый диван. В течение дня Барсик поцарапает диван с вероятностью 0.45, а Мурзик – с вероятностью 0.52. С какой вероятностью к концу дня диван останется нетронутым?
Предполагается, что коты действуют независимо друг от друга.

Решение. Событие A - Барсик не тронул диван в течение дня.
Событие B - Мурзик не тронул диван в течение дня.
Диван к концу дня остался нетронутым - событие AB.

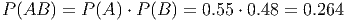
Ответ. P = 0.264.

Комментарий. События «кот поцарапал диван» и «кот не тронул диван» - противоположные. Вероятность одного из них можно получить, вычитая из 1 вероятность другого. Так мы находит P(A) и P(B).

Совместное осуществление событий A и B называется произведением этих событий и обозначается AB.

Коты действуют независимо, поэтому события A и B независимые. Тогда вероятность их произведения можно вычислить по формуле P(AB) = P(A) ⋅ P(B).

Задача 6. На трассе в полдень одновременно стартуют два гонщика: чемпион и новичок. Маршрут гонки состоит из некоторого количества кругов по этой трассе. В 13 часов чемпион опережает новичка на 1.5 круга. Чемпион завершает маршрут в 20 часов, а новичок – в 23 часа того же дня. Сколько кругов проходит новичок за час?

Решение. Пусть маршрут гонки состоит из S кругов, и новичок проходит v кругов в час.
Чемпион проходит v + 1.5 круга в час (он опережает новичка на 1.5 круга в 13 часов, то есть через час после старта).

У новичка: скорость v (кругов в час), время 23 - 12 = 11 ч

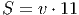
У чемпиона: скорость v + 1.5 (кругов в час), время 20 - 12 = 8 ч

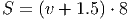
Приравняем:

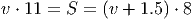
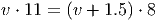
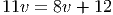
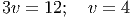
Ответ. 4 круга за час.

Комментарий. Важная идея в этой задаче - выразить расстояние в кругах, а скорость - в кругах в час. Тогда получается, что нужно найти скорость новичка.

Классическую формулу s = v ⋅ t мы применяем два раза: для новичка и для чемпиона. Итого, мы получили два разных выражения для расстояния S. Приравняв эти выражения друг к другу, мы далее исключаем S и получаем уравнение с одной неизвестной v. Так как надо найти именно v, решив уравнение, мы получим ответ.