• Сколько существует четырёхзначных чисел, не делящихся на 1000, у которых первая и последняя цифры чётные?
• Решить систему уравнений в целых числах:
• При каких целых значениях параметра c уравнение + = c имеет хотя бы один корень?
• Дедушка с внуком пошли кататься на лыжах. Отец знает, что по ровному месту оба едут со скоростью 7 км/ч; под году дедушка едет 8 км/ч, а внук - 20 км/ч; в гору дедушка едет 6 км/ч, а внук - 4 км/ч. Оба проехали по одному и тому же маршруту. Может ли отец определить, что больше: протяженность подъемов или протяженность спусков, если первым вернулся дед?
• Решить неравенство:

• Каких чисел от 1 до 1000000 больше: тех, в записи которых есть единица или тех, в записи которых она не встречается?
• Решить систему уравнений в целых числах:
• При каких значениях k число 2 находится между корнями уравнения
  2x² -x + (k - 3)(k + 5) = 0, не совпадая ни с одним из них?
• Дедушка с внуком пошли кататься на лыжах. Отец знает, что по ровному месту оба едут со скоростью 7 км/ч; под году дедушка едет 8 км/ч, а внук - 20 км/ч; в гору дедушка едет 6 км/ч, а внук - 4 км/ч. Оба проехали по одному и тому же маршруту. Может ли отец определить, что больше: протяженность подъемов или протяженность спусков, если первым вернулся внук?
• Решить неравенство:

 

Решения

• Первая цифра числа может быть любой из четырёх (2,4,6 или 8), вторая и третья – любой из десяти каждая, а четвёртая, если отказаться от условия ”не делящихся на тысячу”, - любой из пяти ( 0,2, 4,6 или 8). Следовательно, четырёхзначных чисел, в записи которых первая и последняя цифры чётны, всего имеется 4+10+10+5= 2000; так как среди них четыре числа (2000, 4000, 6000, 8000) делятся на 1000, то чисел, удовлетворяющих условию задачи, окажется 2000 – 4 = 1996.
• Вычтя из второго уравнения первое, получим По условию, x, y, z - целые, тогда возможны два случая:
  • x - z = 1, 1 - y = 1. Т.е. y = 0. Подставив значение y в систему, получим: z = 94, x = 95
  • x-z = -1 , 1-y = -1, т.е. z = x+1, y = 2. Подставив в первое уравнение системы найденные значения, получим: 2x + x + 1 = 94, x = 31. Отсюда z = 32.

  Ответ: x = 95, y = 0, z = 94 или x = 31, y = 2, z = 32.

• ОДЗ: x ∈ [2; 7], c > 0.
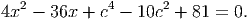
  Возведём в квадрат обе части уравнения: x- 2 + 2 + 7 -x = c²,  тогда 2 = c² - 5, c² ≥ 5, возведём еще раз в квадрат, раскроем скобки, перенесём все в левую часть и получим квадратное уравнение относительно x: Так как это уравнение должно иметь корни, то D ≥ 0: Следовательно, - ≤ c ≤. Тогда ≤ c ≤, c = 3.
• Обозначим протяжённость подъёмов через x, а протяжённость спусов через y. Ровное место можно не учитывать, так как на нём скорости внука и деда одинаковы. Тогда время деда равно а время внука равно Раз первым вернулся дед, то Тогда 9y < 10x, при этом может быть что угодно: y < x, например y = 8, x = 9; y = x, например, y = x = 9; y > x, например y = 11, x = 10.
• Перенесем в одну сторону оба модуля: |x² - 7x + 2|-|x² + 5x- 2|≤ 0. Это неравенство равносильно С помощью метода интервалов определим необходимые промежутки.
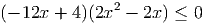
  Ответ: x ∈ [0; ] ∪ [1; +∞)

• Подсчитаем количество чисел от 1 до 999999 (число 1 000 000 содержит единицу, его сразу отбросим), в записи которых нет единиц. Каждую цифру можно выбрать 9 способами (любая цифра кроме 1), поэтому все 6 цифр (по правилу произведения) можно выбрать 9⁶ способами (если в числе до значащих цифр стоят нули, мы их просто отбрасываем). При этом один вариант (000000) нужно убрать, так как число 0 не рассматривается. Получаем всего N = 9⁶-1 = 531440 чисел. Так как всего чисел 1 000 000, то видно, что чисел без единицы среди чисел от 1 до 1 000 000 больше, чем тех, в записи которых единица есть.
• Пусть x - чётно, тогда y - нечётно, а тогда z - чётно и x - нечётно. Получили противоречие. Аналогично, если предположить, что x - нечётно.
  Ответ: Система не имеет решений в целых числах.
• Домножим все уравнение на 2 и раскроем скобки: Напишем корни неравенство на корни уравнения из условия: Раскроем скобки и преобразуем в систему неравенств: Первое неравенство выполняется для любых k, удовлетворяющих ОДЗ для корня. Рассмотрим второе неравенство, возведём его в квадрат и сократим на 32: k²+2k-8 < 0, тогда, решив квадратное неравенство, получим -4 < k < 2.
• Обозначим протяжённость подъёмов через x, а протяжённость спусов через y. Ровное место можно не учитывать, так как на нём скорости внука и деда одинаковы. Тогда время деда равно а время внука равно Раз первым вернулся внук, то Тогда 9y > 10x, тогда y > x, то есть протяжённость подъёмов меньше протяжённости спусков.
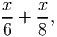
• Заменим неравенство на равносильное При помощи метода интервалов определим промежутки.
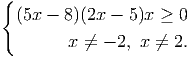
  Ответ: x ∈ [0; ] ∪ [; ∞)